Los Puntos de Lagrange

Tras los avances realizados por Isaac Newton en el campo de la mecánica celeste, el astrónomo, físico y matemático italiano Joseph-Louis Lagrange aportó nuevas claves en el área de la mecánica clásica. Entre los estudios y diversas aportaciones de Lagrange destacan la gravitación de elipsoides; la ecuación secular de la Luna; el movimiento de los nodos de la órbita de un planeta o la estabilidad de las órbitas planetarias.

Pero su principal descubrimiento lo realizó intentando resolver el problema de los tres cuerpos, es decir, las implicaciones matemáticas o físicas que existen entre tres cuerpos en órbita. Se trata de las Ecuaciones de Lagrange, gracias a las cuales se han encontrado los asteroides troyanos y satélites troyanos de Saturno, entre otros avances astronómicos.

Puntos de libración

Los Puntos de Lagrange, que también se denominan puntos L, o puntos de libración, son las cinco posiciones en las que puede estar un objeto pequeño, sólo afectado por la gravedad, en un sistema orbital respecto a dos objetos más grandes. Por ejemplo, sería el caso de un satélite artificial con respecto a la Tierra y la Luna. Los Puntos de Lagrange indican las posiciones donde la atracción gravitatoria combinada de las dos masas grandes proporciona la fuerza centrípeta necesaria para rotar de una forma sincrónica con la menor de ellas.

Los Puntos de Lagrange son similares a las órbitas geosincrónicas, las cuales permiten a un objeto estar en una posición fija en el espacio, en lugar de estar en una órbita en la que su posición relativa cambia continuamente.

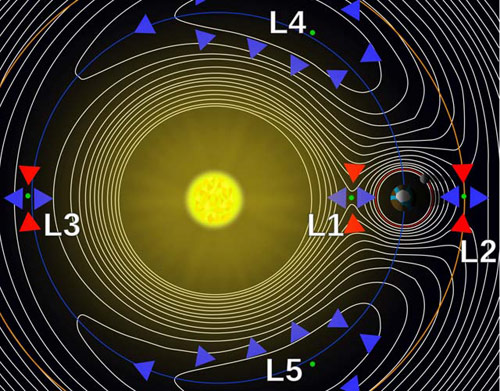
Lagrange reformuló los principios de la mecánica clásica, poniendo un mayor énfasis en la energía, por encima de la fuerza. También aplicó el desarrollo de un método que utilizaba una sola ecuación en coordenadas polares para describir cualquier órbita, incluso aquellas que son parabólicas o hiperbólicas. Dicho método resultó muy útil para calcular el comportamiento de los planetas y cometas. Actualmente también se utiliza para calcular las trayectorias espaciales.